By, Mofazzel Hussain, MSc, BEd.
Chemistry PG Teacher, DBKSSSD
Chapter: Coordination Compounds



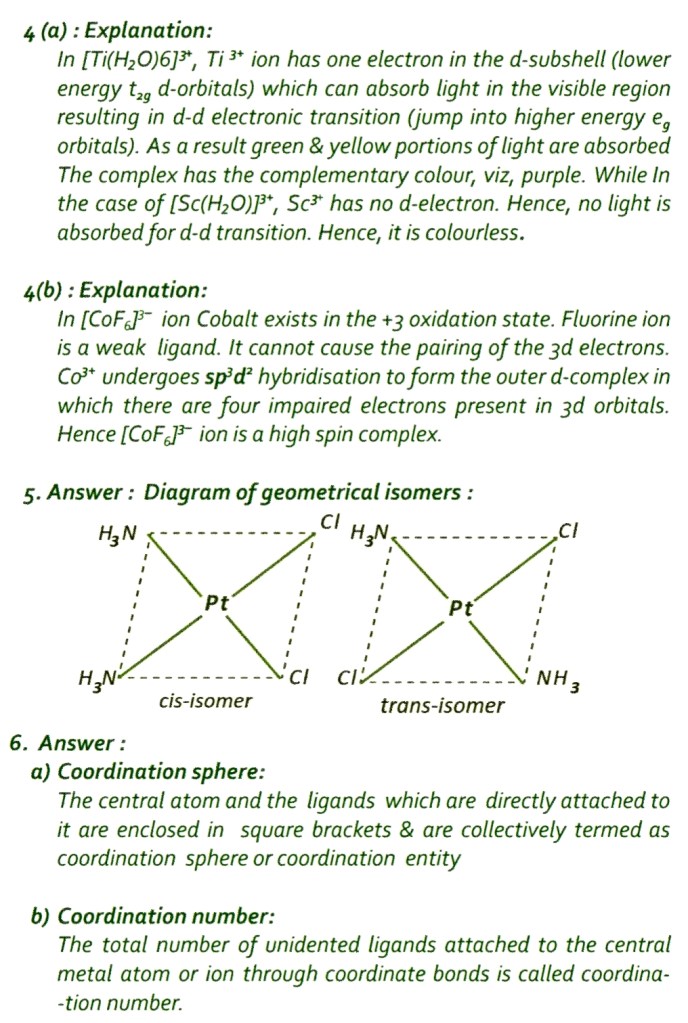


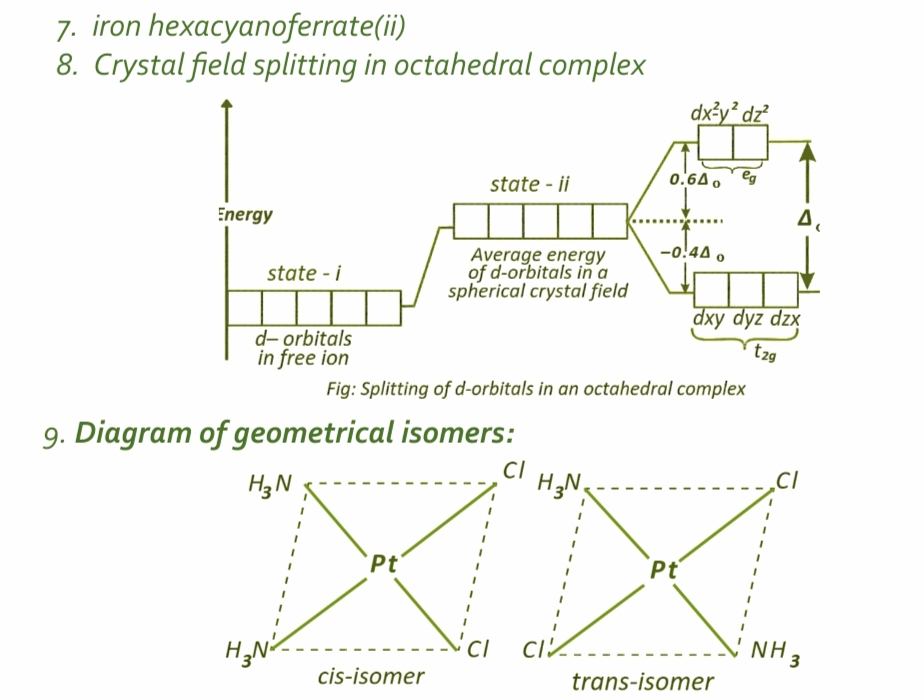

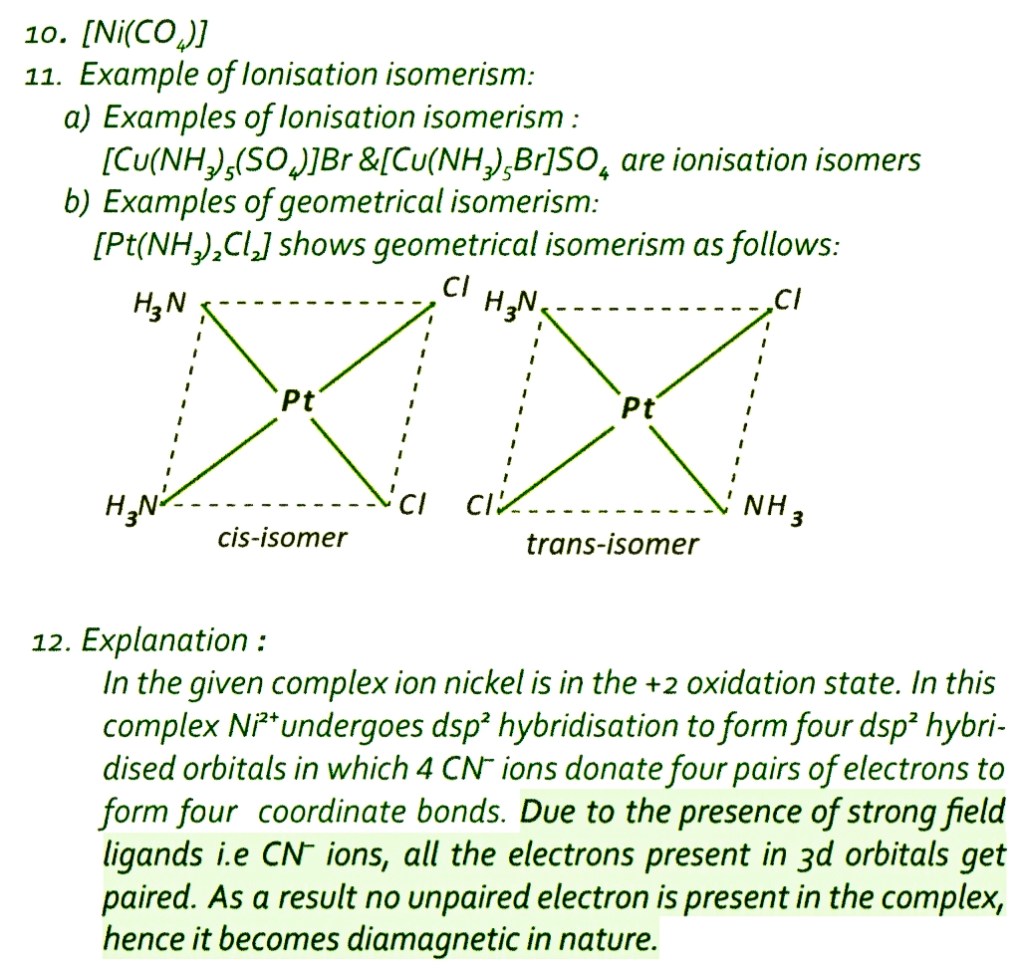
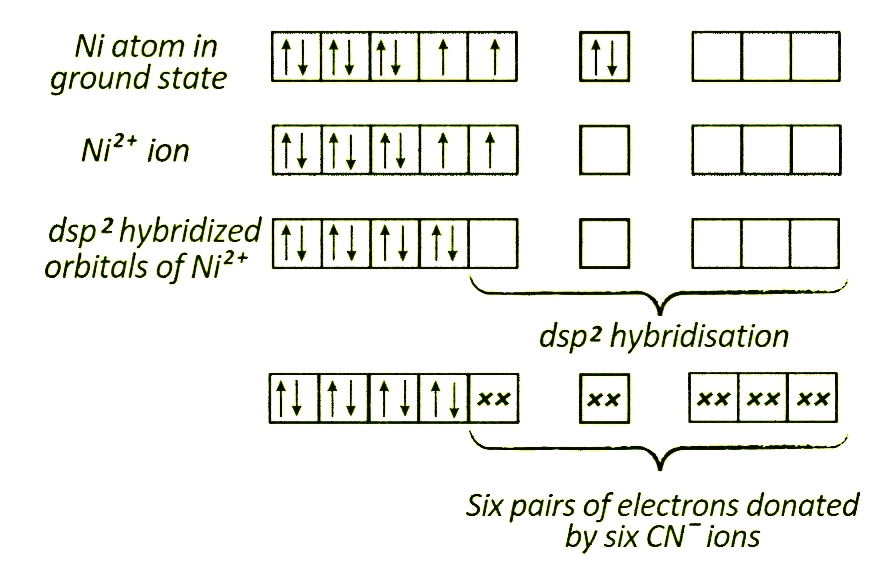











By, Mofazzel Hussain, MSc, BEd.
Chemistry PG Teacher, DBKSSSD
Chapter: Coordination Compounds























Topics to be discussed (As per H.S final year Chem. Syllabus 2022-23)
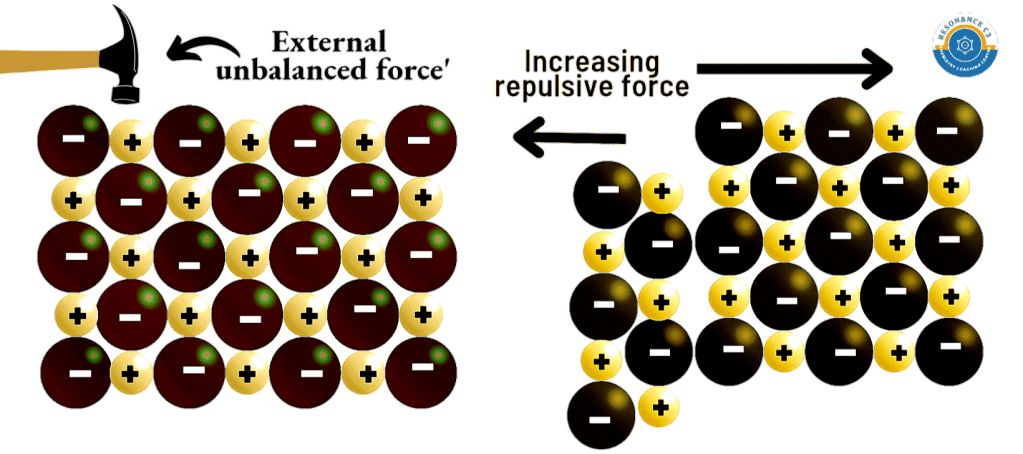
Definition of solid: A solid is defined as that form of physical state, which possesses rigidity and hence possesses definite shape and definite volume.
Based on the arrangement of constituent particles, solid substances are broadly classified into two main categories: a) Amorphous solid and b) Crystalline solids.
Amorphous Solid: A solid is said to be amorphous if there is no regular geometric arrangement of constituent particles. For example rubber, plastic, polymers of high molecular mass etc. exist in this form.
Crystalline solid: A solid is said to be crystalline if its constituent particles are arranged in a definite geometric pattern in three dimensional space. For example, all solid elements of metal and non-metals and their compounds exist in this form.
Some important properties of solids are mentioned below:
Isotropy : In the case of amorphous solids, properties like electrical conductivity, refractive index, thermal expansion etc are identical in all directions. This property is called Isotropy and the solid substance which possesses this property is called Isotropic solid.
Anisotropy: In the case of crystalline solids, properties like electrical conductivity, refractive index, thermal expansion etc have different values in different directions. This property is called Anisotropy and the solid which possesses this property is called Anisotropic solid.
Distinguish between crystalline and amorphous solids :
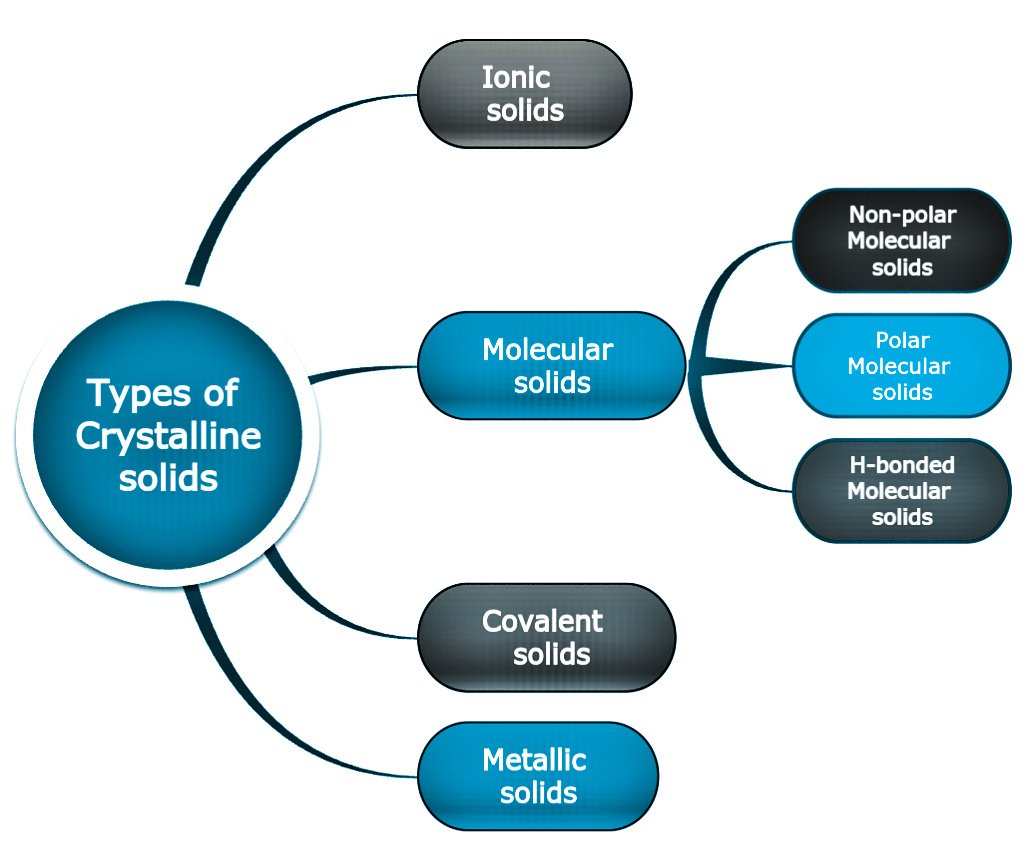
Classification of crystalline solids: On the basis of the nature of particles and binding forces, crystalline solids are further classified into four categories:
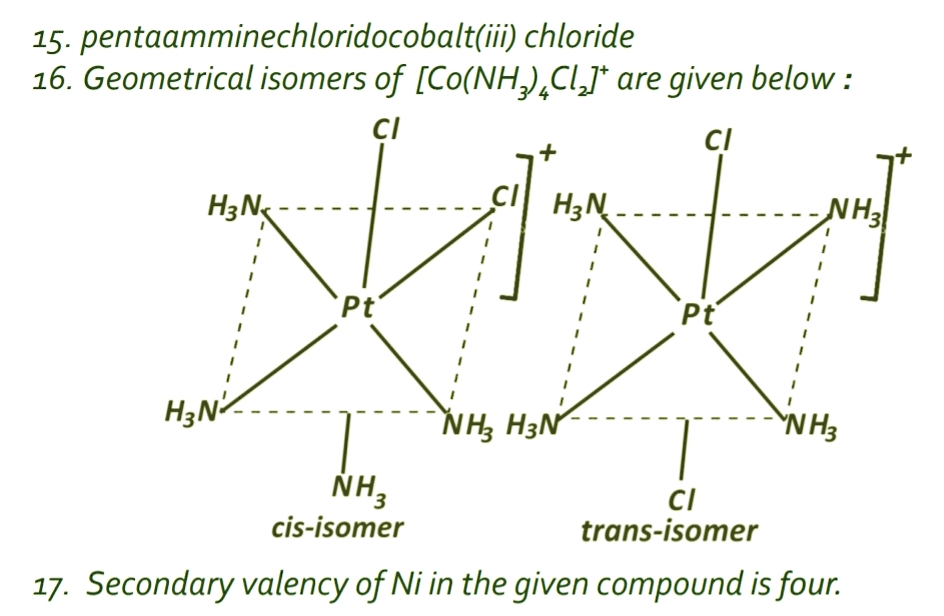
Ionic Solids
Nature of Constituent particles: The constituent particles of ionic solids are ions i.e cations and anions.
Nature of binding force: The oppositely charged ions of an ionic solid are held together by a strong electrostatic force of attraction
Main characteristics :
Molecular Solids
Molecular solids contain molecules as their constituent particles. The binding forces between the molecules are London dispersion forces, Dipole-dipole interaction and Hydrogen bonding.
Depending upon the nature of binding forces molecular solids are further classified into three sub- categories: Non-polar Molecular Solids
a) Non-polar Molecular Solids:
Nature of constituent particles: The constituent particles of these types of solids are non-polar molecules like, diatomic molecules of hydrogen (H2), chlorine (Cl2), Iodine (I2) etc.
Nature of Binding force: The binding force which holds the non-polar constituent particles is London dispersion force.
Main Characteristics:
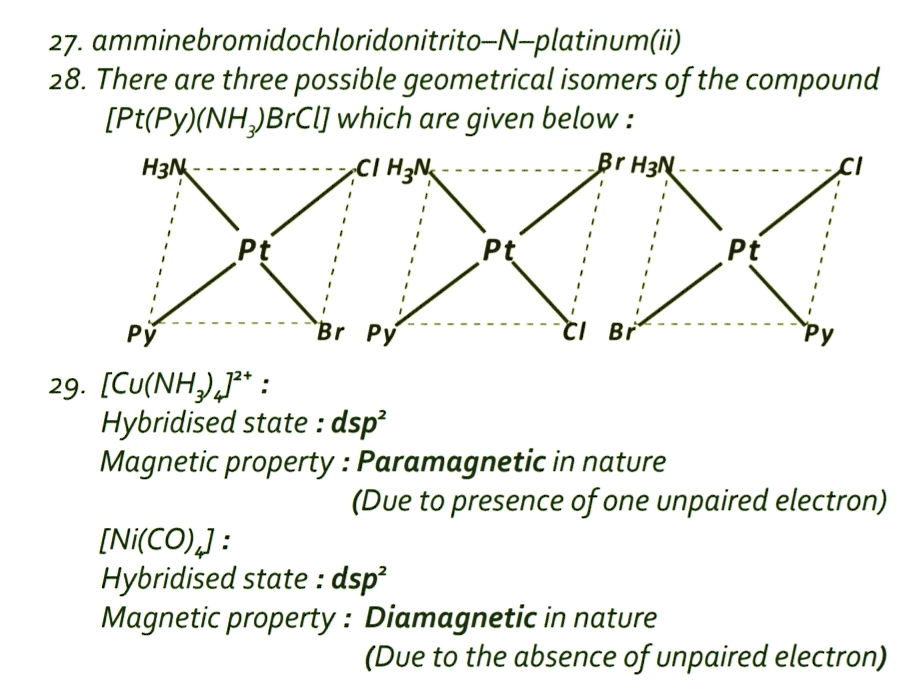
b) Polar Molecular Solids
Nature of Constituent particles: Constituent particles of these types of solids are the polar molecules like hydrogen chloride, sulphur dioxide etc.
Nature of binding force: The constituent particles of these types of solids are held together by Dipole-dipole force of attraction, which is stronger than London dispersion forces.
Main Characteristics
c) H – Bonded Molecular Solids
Nature of particles: The constituent particles of these types of solids are those molecules which can form Hydrogen bonding between them. For example: Water, ammonia etc.
Nature of binding force: The molecules of these solids are held together by intermolecular H-Bonding .
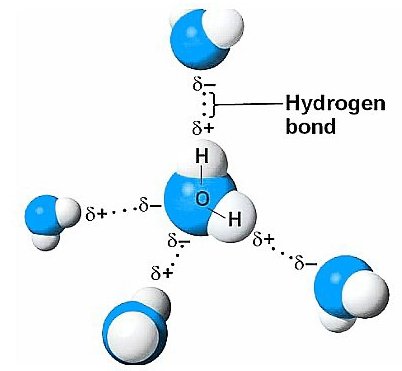
Main Characteristics:
Covalent Solids
Nature of Constituent Particles: The constituent particles of covalent solids are ‘atoms.’
Nature of binding forces: The constituent particles of these types of solids are held together by strong ‘covalent bond force’ .
Example of covalent solids are Diamond, Graphite, Silicon Carbide, Quartz , Boron nitride etc.
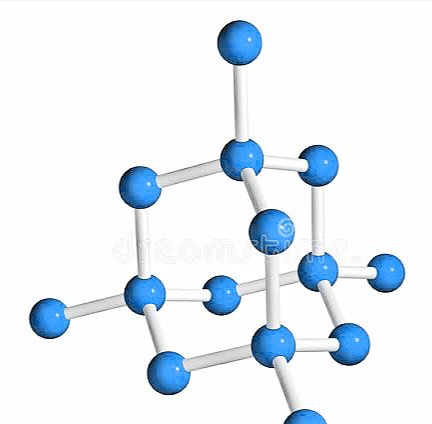
Each carbon atom of diamond is sp3 hybridized. In the crystal lattice of diamond each carbon atom forms four covalent bonds with other four carbon atoms to form a tetrahedral structure. Since all valence electrons are involved in bond formation, so there is no any free electrons in the crystal lattice of diamond. Due to the absence of free electrons diamond can’t conduct electricity.
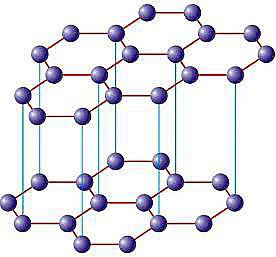
Each carbon atom present in the crystal lattice of Graphite is sp2 hybridized. So each carbon atom forms three covalent bonds with the other three carbon atoms to form hexagonal layered structure. Each carbon contains one free electron in the pure p-orbital. Due to the presence of free electrons it becomes good conductor of electricity.
Two hexagonal layer of sp2 carbon atoms are separated by Vander Waal’s distance. The force of attraction that holds the layers together is very weak in nature. As a result of weak force each layer can slide over another layer. This property makes the crystal slippery in nature. Due to this slippery nature graphite is used as a lubricant in machinery parts.
Main Characteristics
Metallic solids
Nature of particles: Positively charged charged cations and free electrons of the metal.
Nature of binding force: The constituent particles of a metallic solid are held together by strong metallic bonds.
Origin of metallic bonds: In the crystal of a metallic solid, metal atoms release their valence electrons which are loosely held by their respective nuclei, due to their low ionisation enthalpy energy. The free electrons of the metal can move freely in throughout the crystal all directions, like water in the sea. Hence it is also called Sea of free electrons.
The mobile electrons are simultaneously attracted by posotive charged cations, and hence holds positively ions together. The force that holds the metal ions together in the crystal is called metallic bond,
Main Characteristics
Space lattice is a regular repeating arrangement of points . If we consider a small part of the lattice which when repeated in different directions produces the complete space lattice.
Two dimensinoal lattices: A two dimensinoal lattice is a regular arrangment of points in the plane of the paper. We suitably choose four ponts. and connect them to obtain the unit cell.
Types of two dimensinoal lattices
Three dimensional crystal lattice
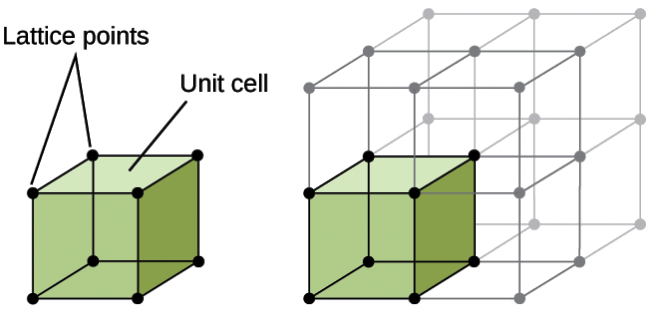
Crystal lattice: The constituent particles of a crystalline solid are arranged in definite geometric pattern in the three dimensional space. Such a regular arrangment of particles is called Crystal lattice.
Some characteristics of a crystal lattice:
Unit Cell: The three dimensional portion of a complete space lattice which when repeated over and again in different directions produces the complete space lattice is called the unit cell.
Types of unit cells: Based on the positions of particles present, unit cells are broadly classified into two main categories: a) Primitive unit cells or simple unit cells b) Non – primitive or centred unit cells.
Primitive unit cells: The unit cells in which the constituent particles are present only at the corners are called primitive unit cells.
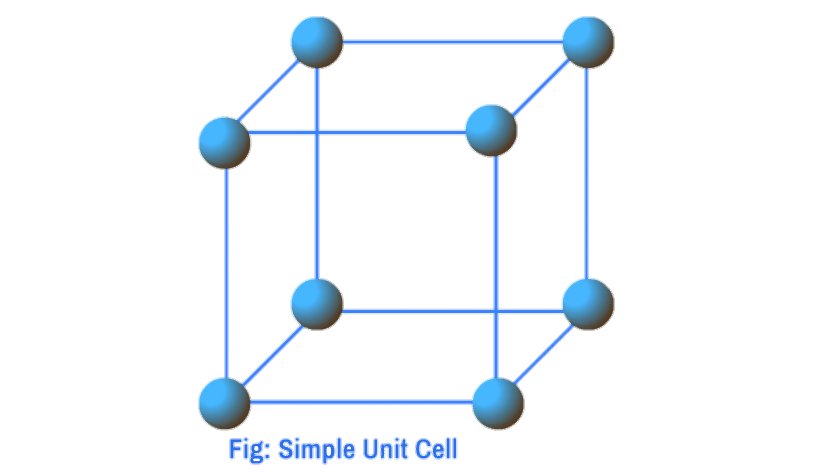
Non – primitive unit cells: The unit cells in which constituent particles are present not only at the corners of the unit cells but also at some other positions are called Non – primitive unit cells . Non – primitive unit cells are further classified into three categories:
Face Centred Cube (FCC) : When in a unit cell constituent particles are present not only at the corners but also at the centre of each face the unit cell is called face-centred cube. (fcc)

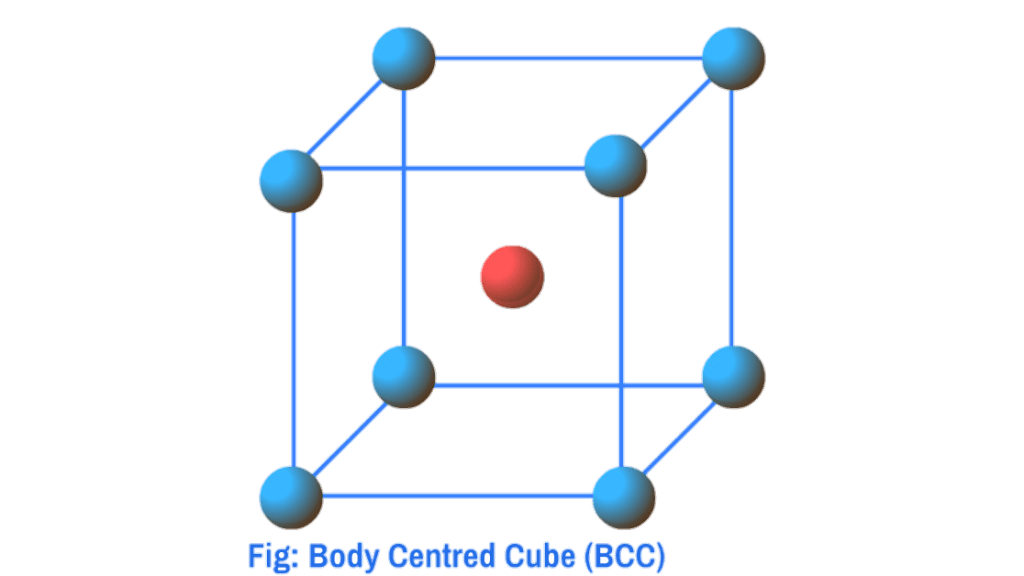
Body Centred Cube (BCC) : When in addition to the particles at the corners, there is one particle present at the centre within the body of the unit cell, it is called body-centred cube (bcc)
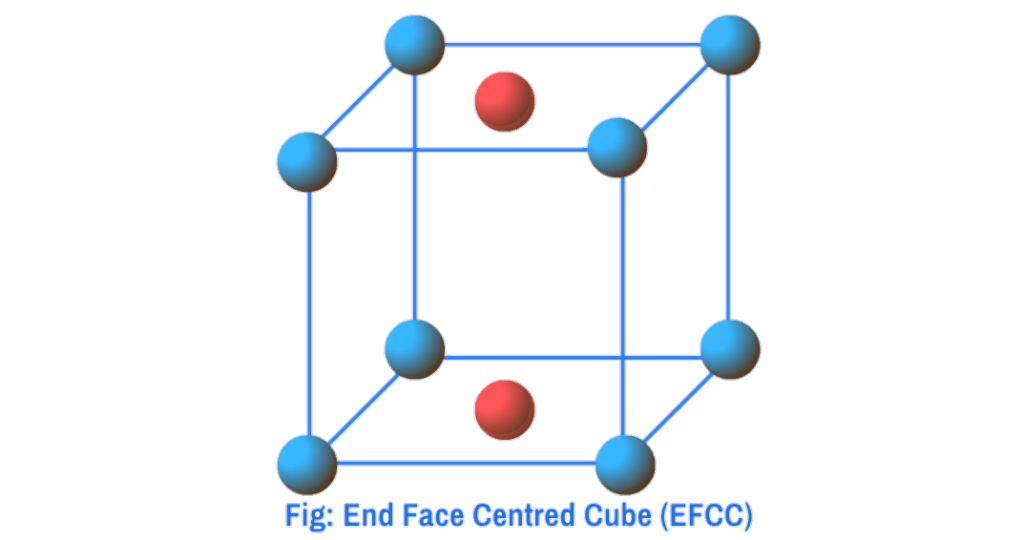
End-face Centred Cube (EFCC) : When in addition to the particles at the corners, there are particles at the centres of any two opposite faces, it is called End-face centred cube (efcc)
Calculation of number of particles present per unit cell:
a) For Simple Cubic Cells:

In the case of a simple cubic cell , particles are present at the corners only. Each corner particle is equally shared by eight unit cells. As a result contribution of one corner particle is 1/8, and the total contribution of eght corners paticles is 8×1/8 = 1. Thus a simple cubic cell contains 1 particle only.
b) Face Centred Cube (FCC)
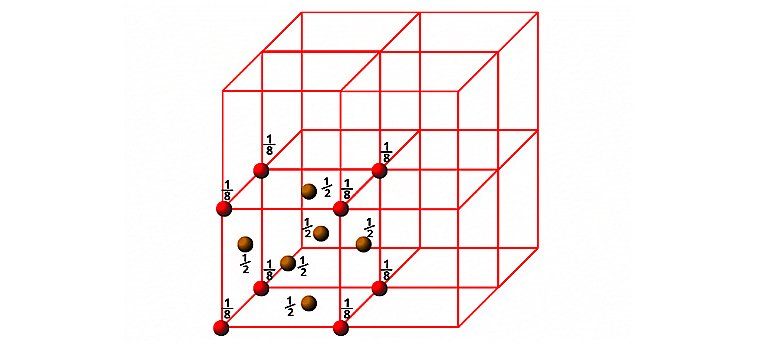
In the case of fcc , particles are present at the corners as well as face centres. Since each corner particle is equally shared by eight unit cells, so contributions from eight corners is equal to 8× 1/8=1. Similarly, since each face centred particle is equally shared by two unit cells, so contributions from six faces = 6×1/2= 3. Therefore, total number of particles present in the fcc unit cell= 1+3=4.
c) Body Centred Cube (BCC)
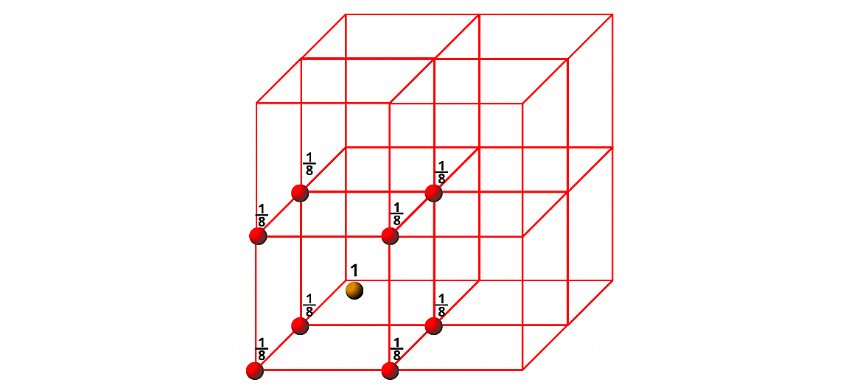
In the case of bcc, particles are present at the corners and one particle is present at the body centre of the unit cell. Since each corner particle is equally shared by eight unit cells so contributions from eight corners = 8×1/8 = 1, and since the body centred particle is not shared by any other unit cells so contribution of body centre = 1. Thus total number of particles present per bcc unit cell is 1+1=2.
d) End Face Centred Cube (EFCC)
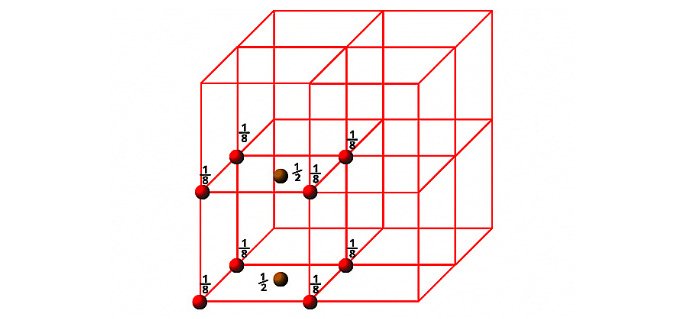
In the case of End-face Centred Cube, in addition to the corner particles there is one particle at the centre of any two opposite faces of the unit cell. Since each corner particle is equally shared by eight unit cells, so contributions from eight corners = 8×1/8 = 1. Similarly, each face centred particle is equally shared by two unit cells, so contributions from two opposite faces is equal to 2×1/2= 1 . Therefore, total number of particles present in an EFCC = 1+1=2.
Relationship between the edge length of a unit cell and radius of particle (Sphere):
For Simple Cubic Cell:
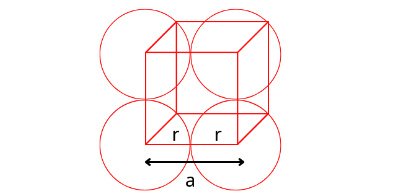
In the case of simple cubic cell, each corner particle is touched by two other corners paticles along the edge length. If each corner particle is represented by a sphere whose radius is ‘r’ and edge length of each edge is ‘a’ , then we can write a = r+r = 2r. or r = a/2

For Face Centred Cube (FCC):

In the case of fcc, the face centred particle touches the corners particles of the same face along the direction of the face diagonal. In the above diagram the face diagonal AB = r + r + r + r = 4r ………….(1) Again from the right angled triangle ABC, the value of diagonal AC can be calculated by Pythagoras theorem, AB² = AC² + CB² therefore, AB² = a²+a² = 2a² => AB = √2a.…………(2)
Now from equations 1 & 2 we get , 4r = √2a, so , r = √2a/4= a/2√2

For Body Centred Cube (BCC):
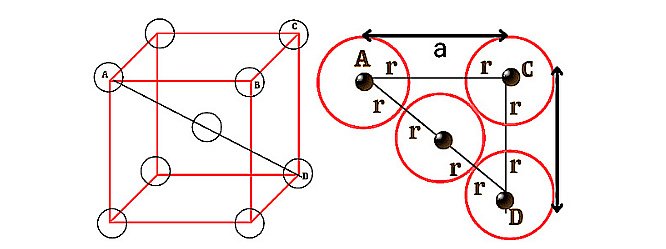
In the case of bcc, the body centred particle touches all the corner particles along the direction of body diagonal. In the above diagram, the value of the body diagonal AD = r+r+r+r = 4r………..(1). If we consider a right angled triangle ABC in the above unit cell, then the face diagonal of the triangle AC²=AB² + BC² => a² + a² = 2a² therefore AC = √2a. Again if we consider the right angled triangle ACD, then the value of its body diagonal AD will be AD² = AC² + CD² => AD² = (√2a)² + a² => AD²= 2a² + a² => AD = √3a ………………(2)
From equations 1 & 2 we get, 4r = √3a, therefore, r = √3a/4.
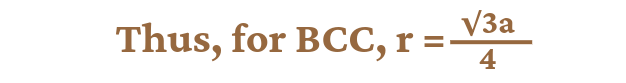
Packing fraction: The percentage of the total space filled by the particles is called Packing Fraction or Packing Efficiency . Mathematically, it is the ratio of volume of particles to the total volume of the unit cell. i.e packing fraction= volume of particles ÷ volume of the unit cell.
Calculation of packing fraction:
Simple Cubic Cell: In the case of a simple cubic cell , suppose the edge length of the unit cell is ‘a’ and ‘r’ is the radius of the particle, then a = 2r. The volume of a spherical particle v′ = 4/3πr³ => v‘ = 4/3 π (a/2)³ => v‘ = a³π/6. Now volume of the unit cell V = a³
Now packing fraction= v‘/V => a³π/6/a³ = π/6 = 0.524 = 52%
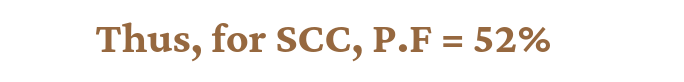
For Face Centred Cube (FCC): In the case of fcc, there are four particles present per unit cell. Since volume of one spherical particle= 4/3πr³ , so volumes of four spherical particles will be v‘ = 4× 4/3πr³ => 16π/3 (a/2√2)³ . (Since for fcc r= a/2√ 2) . Therefore v‘= 16π/a³/16√2. ……. (1)
Again volume of the unit cell. (V) = a³…… (2). Now dividing equation 1 by equation 2, we get , packing fraction= 16πa³/16√2a³ = 0.74 = 74%

Voids in solids
Voids are the empty spaces formed in the lattice structure of solid
Numerical Problems based on the number of particles present per unit cell:
Definition: Any departure from perfectly ordered arrangements of constituent particles in the crystal is called defect or imperfection in solid.
Cause of defects: Defect in solid may arise due to the heat absorption by the crystal or due to the presence of impurities present in the crystal.
Defects are broadly classified into three main categories: a) Point defect and b) Line Defect. But our syllabus contains only the point defect. So here we will study about the point defect only.
When the deviations or irregularities in the ideal arrangement of constituent particles around a point or atom in the crystal, it is called point defect. Point defects are further classified into three categories:
Stoichiometric defects: When imperfections in the solid are such that the ratio between the number of cations and anions is same as represented by the molecular formula of the solid i.e the stoichiometry of the solid is not disturbed, are called stoichiometric defects.
These defects are also called intrinsic defects or thermodynamic defects. These are also two types: a) Vacancy defects b) Interstitial defects.
Vacancy defects: When in a crystalline solids some particles from the latice sites are missing, but the stoichiometric rato between the particles is not disturbed, it is called vacany defect.
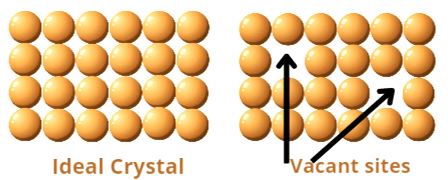
Consequences of vacancy defects : Due to vacancy defects mass of the crystal is decreased but volume of the unit cell remains unchanged. As a result of which, density of the unit cell decreases.
Non – Stoichiometric defects:
